I recently watched a youtube video by Veritasium titled The simplest math problem no one can solve-Collatz conjecture. The Collatz conjecture is a conjecture in mathematics that concerns sequences defined as follows: start with any positive integer n. Then each term is obtained from the previous term as follows: if the previous term is even, the next term is one-half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1(3n+1). The conjecture is that no matter what the value of n, the sequence will always reach 1. 

I was fascinated by this simple sequence that even a fourth-grader can understand. The interesting thing is that mathematicians are yet to solve/prove or disprove. What was more fascinating was how deeply this simple conjecture was rooted in nature, economics, demographics, and even the physical constants. The conjecture is also connected to the Fibonacci numbers. You can get more insight into the Collatz conjecture through this Wikipedia page. 

I decided to attempt coding the Collatz conjecture and graphing out the data, and what better language to use than my newly found best coding partner, Julia. Fair warning though, I’m relatively new to Julia (and programming as a whole) and I’m no mathematician. So don’t expect magic. But for anyone interested in learning to program a basic sequence in Julia or just interested in seeing what this ends in, here goes something. 

After setting up everything (i.e downloading Julia and the required packages such as Plots and IJulia) the first step was writing a simple Collatz_Conjecture function.

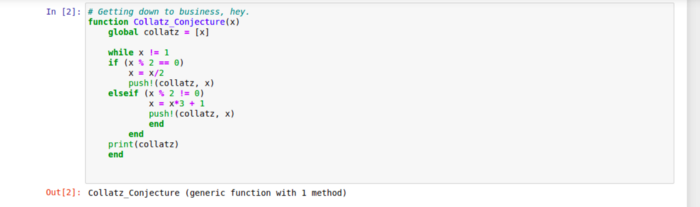
This function is very simple and does four main things:

1. Takes in a variable x and adds it as the first element in an array called Collatz
2. Checks that x is not one (This is because all sequences of these conjecture loop infinitely in the 4–2–1 loop once they reach 1)
3. Checks if x is divisible by two- if it is, it divides x by two and adds the new integer as the second element in the Collatz array)
4. If x is not divisible by two(an odd number), it multiplies x by three, adds one, and adds the new integer to the Collatz array.

The next part is to plot the data in the Collatz array. To do that, I have to create an array with the same number of elements as the Collatz array.

This cell creates an array with the same number of elements as the Collatz array. However, its array elements run from 1, with steps of one(adding one subsequently) to the last element. 

The next part is plotting y against Collatz.

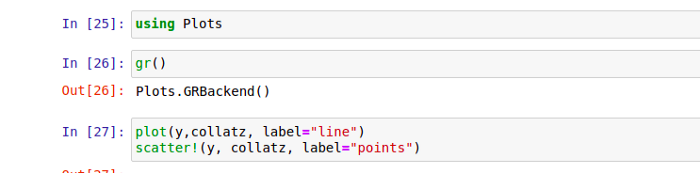
Here is a sample plot for the Collatz conjecture where n=1465018. 

This number has a stopping value(the total numbers it runs through before reaching one) of 120 and its largest value is high above 2.0x10⁶.

And that’s it, a simple way to plot the Collatz conjecture for any positive integer.

The fascinating part about this conjecture was how it related to nature and our society at large. I won’t go deeply into the intricacies but I will give you a taste of its interconnectedness. 

Still using the same number 1465018, I wrote a code to take the logarithms of all the numbers in its Collatz array and push the results to a new array, p.

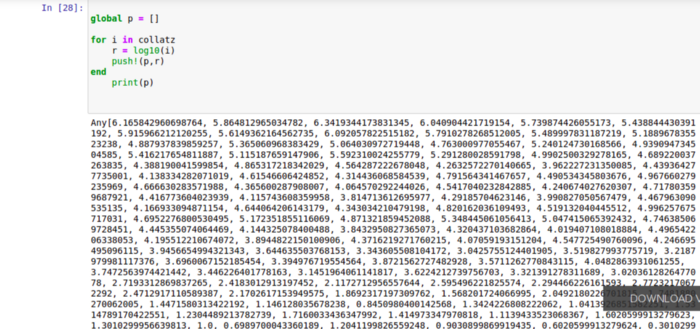
Plotting y against p, the result was what looked like the stock market on a bad day. 

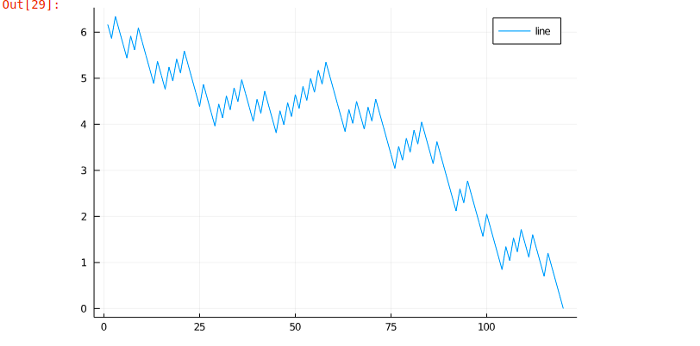
This clearly shows how such a simple sequence can find its way into some of our most ‘complex’ systems. This downward distribution of data that is commonly observed in countries’ inflation, the value of companies, and all the physical constants constitute Benford’s law. The law states that the leading digit is likely to be small in many naturally occurring collections of numbers. In sets that obey the law, the number 1 appears as the leading significant digit about 30 % of the time, while 9 appears as the leading significant digit less than 5 % of the time. 

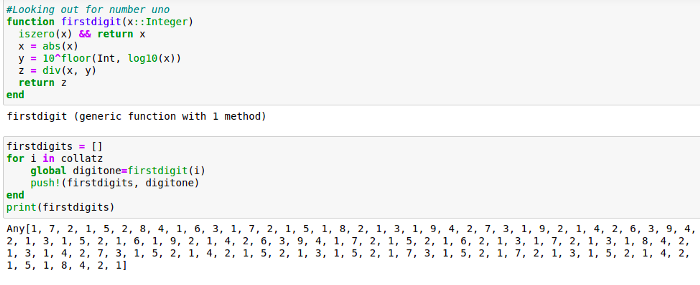
Writing a function that takes returns the first number of any integer took me quite a while but thanks to the friendly contributors at the Julia discourse community, I was able to write a function that did just that. I then took the first digit of every element in the Collatz array and added them to a new array called firstdigits. 

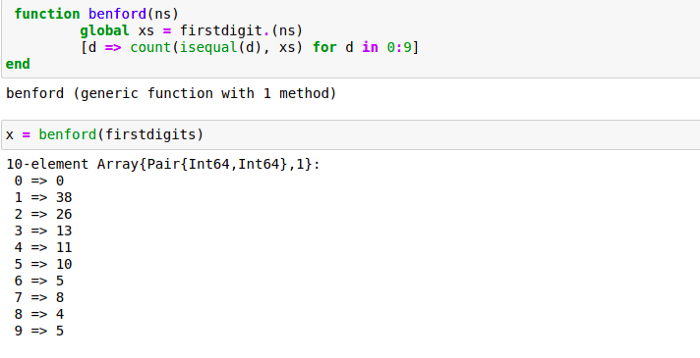
The last part counted the total number of appearances for every digit in the firstdigits array and plotted the digits from 0 to 9 against their number of appearances. 

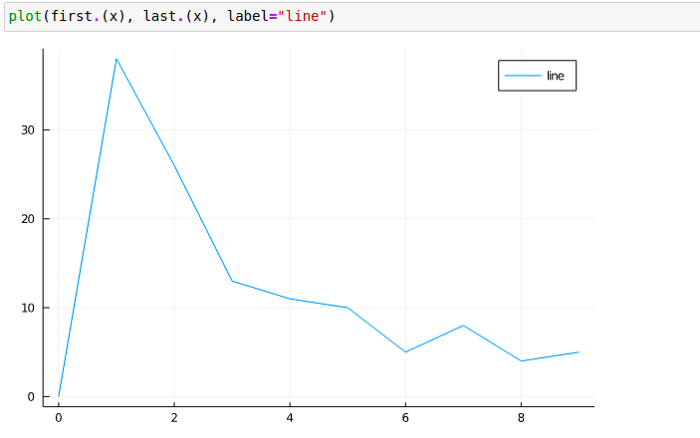
And this is the final result for the number 1465018 showing clearly Benford’s law. 

Another fascinating thing that can be done using the Collatz conjecture is to create organic-looking shapes the means of a directed graph, but that’s a code for another day! 

Working on this mini-project helped me better understand the Julia language but more so into the beauty of math and nature, and I thank God for it.